CRYSTALS - Kyber Compression and KEM
Post-quantum algorithm CRYSTALS Kyber KEM and variable compression explained.

Introduction
We have defined the core of CRYSTALS-Kyber algorithm in the previous article. The implementation is very bare bones version and there is room for optimization. Encryption algorithms are used in massive counts and how they perform matters to whole internet audience. This motivates to fine-tune the algorithm and protocols to the highest level.
We will introduce the compression of \(A\), \(u\) and \(v\).
We will also introduce (a variant of) Fujisaki-Okamoto transform that will secure the key exchange process against chosen-ciphertext attacks. FO-transform will extend the PKE-scheme to a full KEM-scheme.
The Kyber standard FIPS 203 goes to lengths defining the highly sophisticated algorithms used. Here we settle to introduce and implement only the basic idea.
The number theoretic transform (NTT), which is used to speed up the polynomial multiplication, is complex enough to be handled separately later on.
Size analysis
Kyber comes with three separate recommended configurations.
| Name | n | q | k | eta1 | eta2 | du | dv |
|---|---|---|---|---|---|---|---|
| ML-KEM-512 | 256 | 3329 | 2 | 3 | 2 | 10 | 4 |
| ML-KEM-768 | 256 | 3329 | 3 | 2 | 2 | 10 | 4 |
| MK-KEM-1024 | 256 | 3329 | 4 | 2 | 2 | 11 | 5 |
Here \(d_u\) and \(d_v\) are new parameters that are related to compression defined later in this article. The standard also defines the strength of used (pseudo) random number generators, but we'll skip that.
Consider now the configuration ML-KEM-768. Here \(q=3329\) which means we need at least 12 bits to represent it. Since \(k=3\), the matrix \(A\) is \(3\times 3\) and hence holds \(9\) polynomials each with \(n=256\) coefficients. These total to \(12\times 9\times 256=27648\) bits meaning \(3456\) bytes. The vector \(t\) is of size \(3\) elements hence taking \(3\times 9\times 256=6912\) bit, i.e. \(864\) bytes. This means the public key \((A,t)\) takes total \(3456+864=4320\) bytes.
While \(4320\) bytes may not seem much, it's significantly larger than keys used in current non-PQ algorithms. This calls for compression.
Compression of Matrix A
We can compress matrix \(A\)'s coefficients using a clever trick: instead of transmitting all coefficients, we only share a random seed to generate them. This works through an extendable output function "XOF".
XOF works like a pseudo-random number generator. When initialized with a seed, it always produces the same sequence of values. If both Bob and Alice use the same algorithm with same seed, they'll generate identical values.
We share just a 256-bit seed and use SHAKE128 to generate the actual coefficients of \(A\) in a predefined way. As we only share the 256-bit seed, we reduce \(A\)'s size from 864 bytes to just 32 bytes.
We implement this in the PolyMatrix class as a separate method fill_xof. The CRYSTALS-standard defines a specific sampling procedure, but we'll implement just the main idea.
def fill_xof(self, seed):
""" Fill the matrix with values extracted from SHAKE128
with the given seed. The values are extracted by two
bytes at a time, putting the limit of q to 2^16."""
coefficients = []
shake = hashlib.shake_128()
# Initialize XOF with the seed. Now each party uses this same
# method and since SHAKE128 is fully deterministic, they end
# up with the same coefficients.
shake.update(seed)
bytes_per_number = 2 # This puts a limit on size of q
random_bytes = shake.digest(self.rows*self.cols*self.n*bytes_per_number)
for i in range(0, len(random_bytes), bytes_per_number):
val = int.from_bytes(random_bytes[i:i + bytes_per_number], byteorder='little')
coefficients.append(val % self.q)
# Populate the matrix entries. Extract values for a polynomial
# and use that to instantiate a new polynomial.
for i in range(self.rows):
for j in range(self.cols):
new_coefficients = coefficients[0:self.n]
coefficients = coefficients[self.n:]
self[i, j] = ZqPolynomial(self.q, new_coefficients)
return self
Now we just need to generate the secret and transfer it instead of full matrix \(A\).
self.A = secrets.token_bytes(32)
self.A_matrix = PolyMatrix(self.kyber_params.k, self.kyber_params.k, self.kyber_params.q, self.kyber_params.n)
# Now others_a is the seed that we use to construct matrix A
self.A_matrix = self.A_matrix.fill_xof(self.A)
The "randomness" of \(A\) now suffers a bit. There are only \(32\) random bytes left from the initial (whopping) \(3456\) bytes. But this has been estimated by the crypto community to be enough.
Vector \(t\) is not compressed.
Compression of u and v
Earlier we mentioned the parameters \(d_u\) and \(d_v\). These are used to compress \(u\) and \(v\) respectively.
The compression technique itself is rather simple. We map the values of the coefficients of \(u\) and \(v\) to a smaller domain. In Kyber the compression is defined as a map \[ \text{Compress}(x,d)=\lceil \frac{2^dx}{q}\rfloor\bmod 2^d\] and the decompression as inverse mapping \[ \text{Decompress}(x,d)=\lceil\frac{qx}{2^d}\rfloor.\] The compression scheme extends naturally to modules.
We can implement this in Zq and make cascading calls from ZqPolynomial and PolyMatrix as we did with rounding. (Notice that FIPS 203 specifically forbids using any floating point arithmetic...)
def compress(self, d):
self.value = round((2**d / self.q) * self.value) % 2**d
return self
def decompress(self, d):
self.value = round((self.q / 2**d) * self.value) % self.q
return self
When testing this you might notice that decompress almost always returns different coefficient values than the original. This might cause some concerns on if we can really loose information this way.
It can be proved that for \(x\in [0,q-1]\) and \[x'=\text{decompress}(\text{compress}(x,d),d)\]we have\[\|x'-x\|_{\infty}\leq \lceil q/2^{d+1}\rfloor.\]
Hence the error is always limited. The way the compression is done is pretty clever, it just "discards" the low-level bits.
As it happens, we can and the net effect is not a problem. Recall the decrypt \[\text{Round}(v-s^Tu).\] With the compression we now introduce \(u\) and \(v\) small errors \(\Delta_u\) and \(\Delta_v\). This means the decrypt becomes \[\text{Round}((v+\Delta_v)-s^T(u+\Delta_u)).\]The error introduced is small and since we are already rounding, the total effect is negligible. It does introduce some error potential, but that is already included in the estimates we provided earlier.
KEM-scheme
The PKE (public-key encryption), that we now have covered, is built against chosen-plaintext attacks. But we need to ensure also, that the full scheme is secure against chosen-ciphertext attacks, too. We accomplish this via a (variant of) Fujisaki-Okamoto transform.
Notice that the full FO-transform is implemented in the Person-class methods encrypt_kem and decrypt_kem. The encrypt and decrypt just implement the PKE-scheme without KEM.
Alice has how established her public key as \((A,t)\).
Bob first samples a random vector \(m\) following the earlier implementation.
Then Bob concatenates \(A\) and \(t\). We implement this with a direct concatenation of the coefficients implemented in method concatenate_matrices. Then we hash the concatenated string with sha3_256 and store the result in \(h\), which is now \(256\) bit byte-object.
at_concatenated_string = self.concatenate_matrices(others_a_matrix, others_t)
# This is H function
sha3_256 = hashlib.sha3_256()
# Encode the concatenated string to a byte string
sha3_256.update(at_concatenated_string.encode('utf-8'))
h = sha3_256.hexdigest()
Then we continue with hashing, and compute the hash of \(m\) and \(h\) concatenated. Notice that we transform \(m\) to bytes.
m_bytes = bytes(m)
h_bytes = bytes.fromhex(h)
mh_concatenated = m_bytes + h_bytes
# This is G function
sha3_512 = hashlib.sha3_512()
sha3_512.update(mh_concatenated)
random_value = sha3_512.hexdigest()
We have now the variable random_value that has 512 bits. We chop it to two pieces, \(K\) and \(R\). Now \(K\) is the private symmetric key, and NOT the m which we used as a symmetric key earlier. The way \(K\) is now constructed provides better randomness.
Notice that the process so far is fully reproducible, i.e. we did initialize the hash functions with known values meaning that we can run each step again and get identical results (assuming \(m\) is constant).
We use now \(R\) as a source to sample the coefficients of \(r\), \(e_1\) and \(e_2\). To do this, we utilize SHAKE256 which we initialize with \(R\). The python implementation is a bit hairy, because I couldn't come up a way to track down the state of shake while filling the coefficients.
We need to fetch all bytes from SHAKE256 upfront, which calls for some pre-calculations.
shake = hashlib.shake_128()
shake.update(bytes.fromhex(R))
# We need to extract the amount of bytes needed upfront and pass the
# value to subsequent method calls. It seems shake_128 does not have
# a way to extract bytes as we go.
bytes_for_eta1 = 1 + (self.kyber_params.eta1//8)
bytes_for_eta2 = 1 + (self.kyber_params.eta2//8)
bytes_r = self.kyber_params.k * self.kyber_params.n * bytes_for_eta1
bytes_e1 = self.kyber_params.k * self.kyber_params.n * bytes_for_eta2
bytes_e2 = self.kyber_params.n * bytes_for_eta2
bytes_sampled = shake.digest(2*(bytes_r + bytes_e1 + bytes_e2))
We then use the xof-functions of PolyMatrix, which cascades to xof-function of ZqPolynomial, which further cascades to Zq, where the implementation is as follows.
@classmethod
def random_binomial_xof(cls, q, eta, bytes_to_use):
""" Return Zq instance with value sampled from CBD. bytes_to_use is
expected to have the random bits that is used in the sampling process.
"""
# For secret/error terms
bytes_needed = (eta // (8) ) + 1
bits1 = []
bits2 = []
int_value = int.from_bytes(bytes_to_use[0:bytes_needed], byteorder='big')
for i in range(eta):
bits1.append( (int_value >> i) & 1)
int_value = int.from_bytes(bytes_to_use[bytes_needed:], byteorder='big')
for i in range(eta):
bits2.append( (int_value >> i+1) & 1)
value = sum(bits1) - sum(bits2)
result = cls(q,value)
result = result.to_symmetric()
return result
Then we proceed as earlier by computing \(u\) and \(v\).
m_new = [int((self.kyber_params.q / 2) * x + 0.5) for x in m]
#m is polynomial, but we pack it to a matrix for smooth arithmetics
m_matrix = PolyMatrix(1, 1, self.kyber_params.q, self.kyber_params.n)
m_matrix[(0, 0)] = ZqPolynomial(self.kyber_params.q, m_new)
v = others_t.T @ self.r + self.e2 + m_matrix
u = others_a_matrix.T @ self.r + self.e1
u = u.compress(self.kyber_params.du)
v = v.compress(self.kyber_params.dv)
The ciphertext is now \(u,v\) as it was before, but remember that \(K\) is the secret and not \(m\).
In the decrypt phase we first extract \(m\) from \((u,v)\) as we did before. Now you remember that the process we implemented above, is fully reproducible, hence we can reconstruct \(u\) and \(v\). And that is what we do.
Let the reconstructed ciphertext be \(u',v'\). If after the reconstruction we have either \(u\neq u'\) or \(v\neq v'\), we have a reason to believe the message was tampered and hence we take the decryption to have failed.
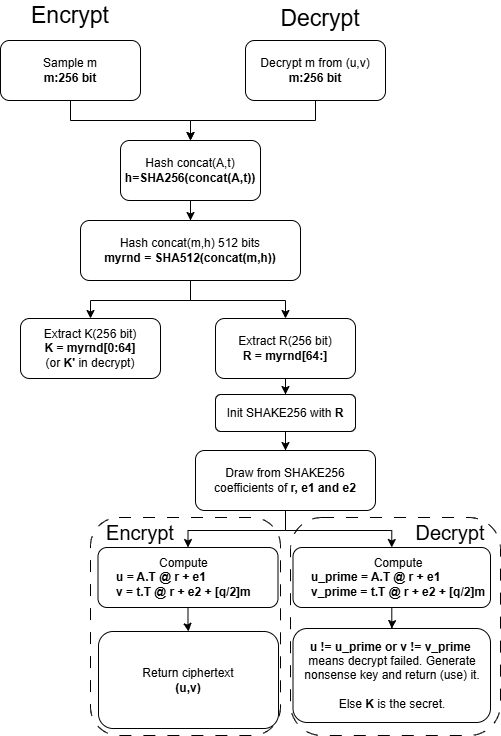
The full flow is above. The code includes some (a lot...) duplicate rows, but I wanted to keep the encrypt and decrypt isolated.
Next steps
As noted, the NTT is a bit involved and I need to think how to present it. But I'm working on it and will publish it hopefully soon.
